論文解説 Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer (MoE)
こんにちは Ryobot (りょぼっと) です.
本紙は ICLR 2017 のポスターセッションでもっとも注目を集めた論文である.写真の右側の Google Tシャツの男性が第一著者の Noam Shazeer,左側の女性が第二著者の Azalia Mirhoseini (ソース).
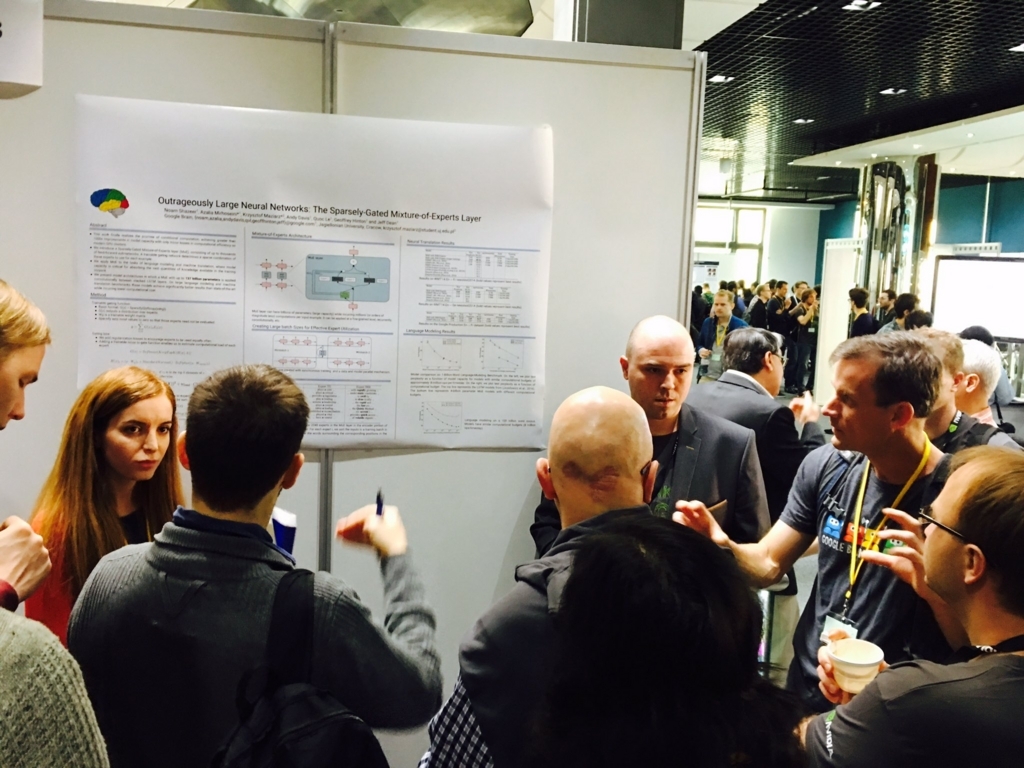
この論文では傍若無人なほど巨大な (Outrageously Large) 混合エキスパートと少数のエキスパートを選択するゲーティングネットワークを用意し,ゲーティングで選択した少数のエキスパートのみ順/逆伝播を実行することで巨大なモデルであっても少ない時間で訓練できる.機械翻訳と言語モデルの SOTA を達成した.
著者に猫の概念で注目を集めた Quoc Le,深層学習のゴッドファーザー Geoffrey Hinton,分散システムの大御所 Jeffrey Dean が会している点でも注目を集めた.
WMT'14 の BLEU スコアは英仏: 40.56, 英独: 26.03 で第 3 位 (登場時 1 位)
- Outrageously Large Neural Networks: The Sparsely-Gated Mixture-of-Experts Layer [Noam Shazeer, Quoc Le, sec-last: Geoffrey Hinton, last: Jeffrey Dean, ICLR'17 Poster, arXiv, 2017/01]
- TensorFlow (著者ら)
最大で 13 万個のエキスパート (パラメータは 1370 億!) の混合エキスパートを使用している.比較として 34 層の ResNet のパラメータは 360 万,人間の大脳皮質のニューロン (ユニット) は 100 億,シナプス (パラメータ) はその 1 万倍の 100 兆である.
条件付き計算
昨今の深層学習ではデータ量が無尽蔵に存在するなら「モデルサイズは大きければ大きいほど性能が良い」という教義がまことしやかに囁かれ,特に Google はこの宗教を強く信仰している.さて仮に「巨大なデータセットで巨大なニューラルネットを学習すれば最強!」だとして,現実問題としてデータサイズとモデルサイズが同時に大きくなれば計算時間が 2 乗オーダーで増えるので今まで実行に移すことが困難であった.これを解決する手段の 1 つが条件付き計算 (Conditional Computation) である.
- Estimating or Propagating Gradients Through Stochastic Neurons for Conditional Computation [Yoshua Bengio, arXiv, 2013/08]
- Exponentially Increasing the Capacity-to-Computation Ratio for Conditional Computation in Deep Learning [Kyunghyun Cho, last: Yoshua Bengio, arXiv, 2014/06]
条件付き計算は深層学習御三家の 1 人 Yoshua Bengio が提案した手法である.条件付き計算では学習データごとにネットワークの一部を有効もしくは無効に切り替える.ゲーティングの方法はバイナリ・スパースを問わず,連続的・確率的・決定論的も問わない.ゲーティングを学習するために強化学習や誤差逆伝播のアプローチが提案されている.
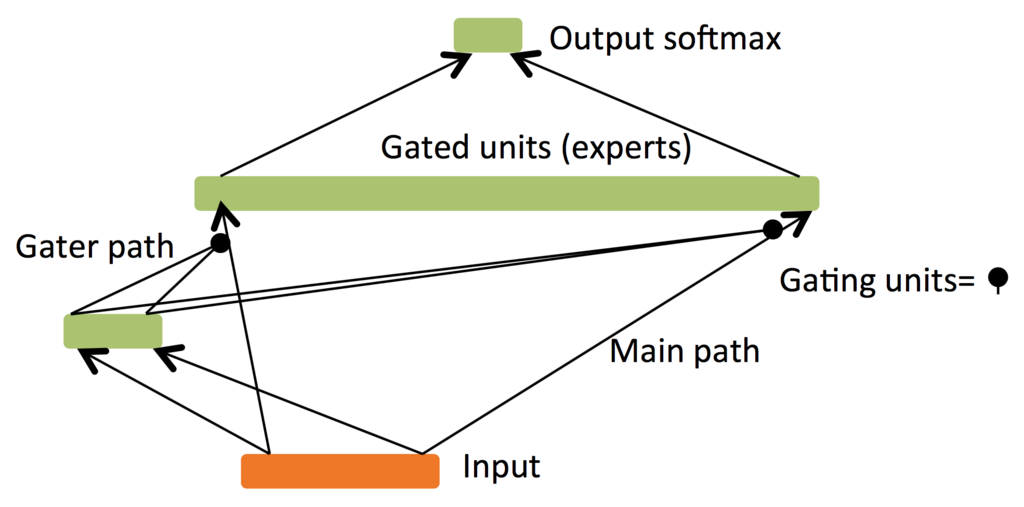
上図 [Bengio, 2013] は左のゲーティングパスが疎な出力 を生成し,エキスパートの出力
と要素ごとの積を求める.
混合エキスパート
混合エキスパート (Mixture of Experts, MoE) は分割統治法 (Divide and Conquer Method),つまり複雑な問題を分解して簡単なサブ問題を解決する戦略を志向したモデルである.起源は Geoffrey Hinton の研究グループが提案した混合エキスパート [Jacobs, 1991] である.
- Adaptive Mixtures of Local Experts [Robert A. Jacobs, sec: Michael Jordan, last: Geoffrey Hinton, 1991]
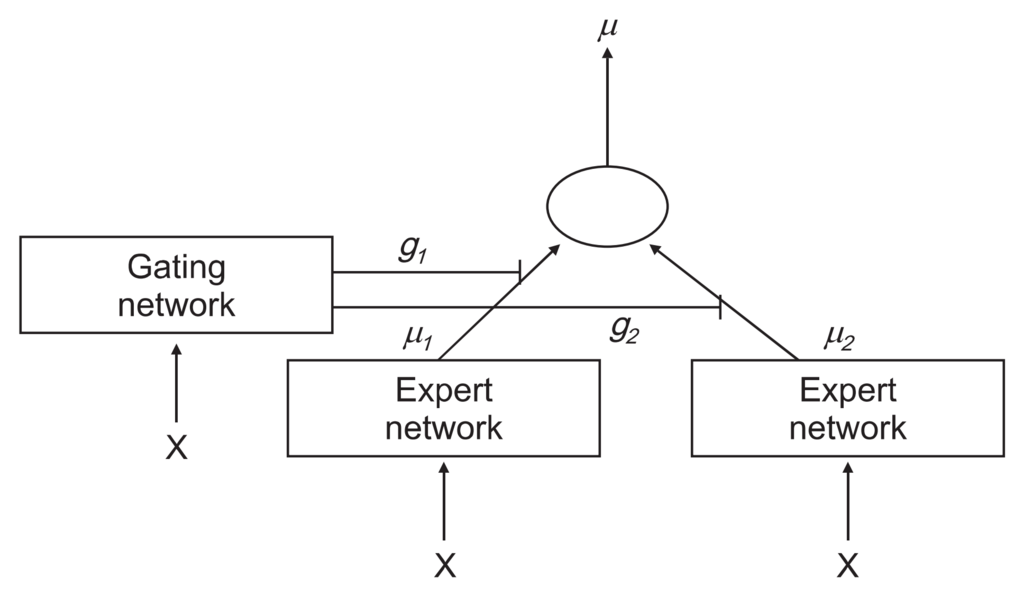
混合エキスパートは 個のエキスパートネットワークの集合
と
次元ベクトルを出力する
個のゲーティングネットワーク
から構成される.全てのエキスパートの入力サイズと出力サイズは同じでなければならないが,各エキスパートは異なるネットワークを使用できる.ここでは同じ構造のフィードフォワードネットワークを使用する.
入力 を与えた時のゲーティングネットワークの出力を
,
番目のエキスパートネットワークの出力を
とする.混合エキスパートの出力
は次式によって表される.
これはゲーティングネットワークの出力 (ベクトル) と全エキスパートの出力 (行列) の内積に等しく,各エキスパートの出力を加重和している.
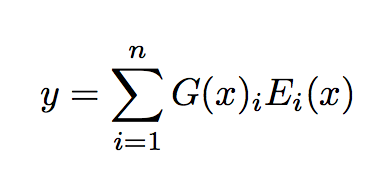
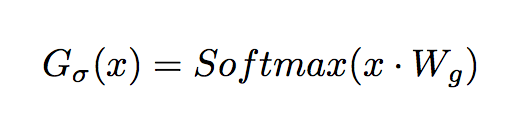
本紙では混合エキスパートを機械翻訳に適応している.類似した取り組みに Mixture of NMT Experts [Garmash, 2016] がある.
- Ensemble Learning for Multi-Source Neural Machine Translation [Ekaterina Garmash, ACL, 2016]
スパースゲーティング
スパースゲーティング (Sparse Gating) は,疎な 次元ベクトルを出力するゲーティングネットワーク
を使用し,出力
のスパース性をもとに計算を節約する.つまり
に対応する
は計算する必要がない (順伝播は
がかけられ特徴が消え,逆伝播も
がかけられ勾配が消えるため).
よって仮に数千のエキスパートを使用しても各標本で計算に使用するエキスパートは少数に限られる.

スパース性のない通常のゲーティングネットワーク [Jordan, 1994] は ソフトマックスゲーティング (Softmax Gating) と呼ばれ,次式のように入力 と学習パラメータの重み行列
の内積にソフトマックス関数を適応する.
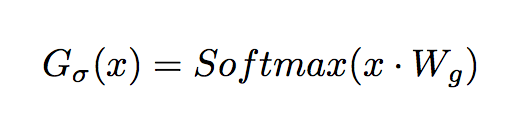
著者らはソフトマックスゲーティングにスパース性とノイズを加えたノイジーな上位 K ゲーティング (Noisy Top-K Gating) を提案している.
まず重み行列 によってノイズ量を学習できるガウスノイズ (標準正規分布に従うノイズ) を各エキスパートネットワークの出力に加える.次に
関数によって上位
の成分の値のみ保持し他の成分の値を
に飛ばすことで,ソフトマックス関数を適応した出力
のうち対応する成分の値を
にする.

スパース性は計算を節約し,ノイズは負荷分散に貢献する.理論上はスパース性によってゲーティングネットワークの出力に不連続な点を生成するが,実践上は問題にならない.
のうち上位 k 成分の値は非ゼロの導関数が得られるので,ゲーティングネットワークの重み
は単純な逆伝播で学習できる.ブーリアンゲーティングと強化学習を用いた訓練方法 [Bengio, 2015] もある.
Softplus 関数は ReLU のヒンジ付近をなめらかにした活性化関数である.余談だが Softplus の導関数はシグモイド関数であり,Softplus - ReLU は y 軸で線対称な曲線になる (参考).
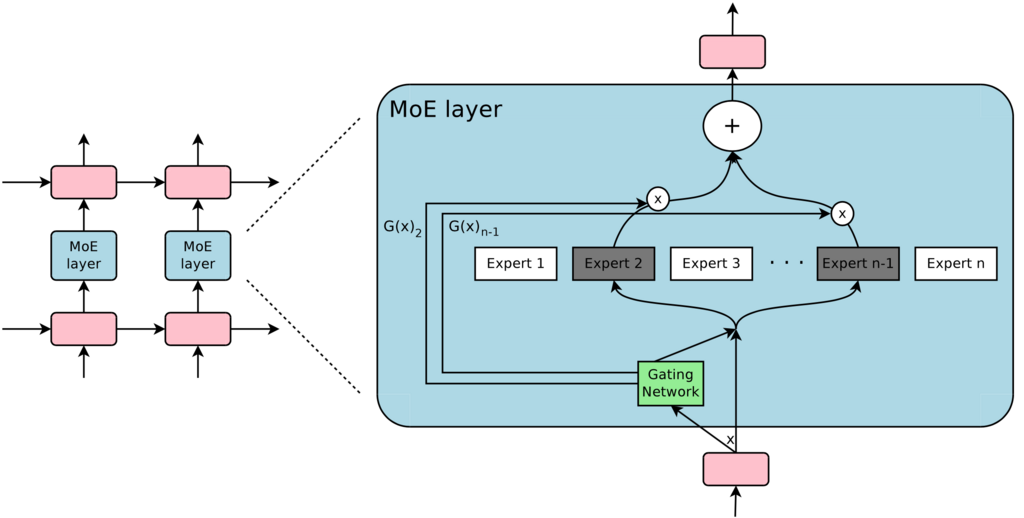
言語モデルと機械翻訳ではテキストの各位置の単語が 2 層の LSTM 間に挿入した混合エキスパート層に入力され,ゲーティングネットワークによって単語ごとにエキスパートの異なる組み合わせが選択される.
ここで混合エキスパートの興味深い性質を紹介したい.
混合エキスパートを学習すると各エキスパートは特定の構文や意味を処理するように専門化される.
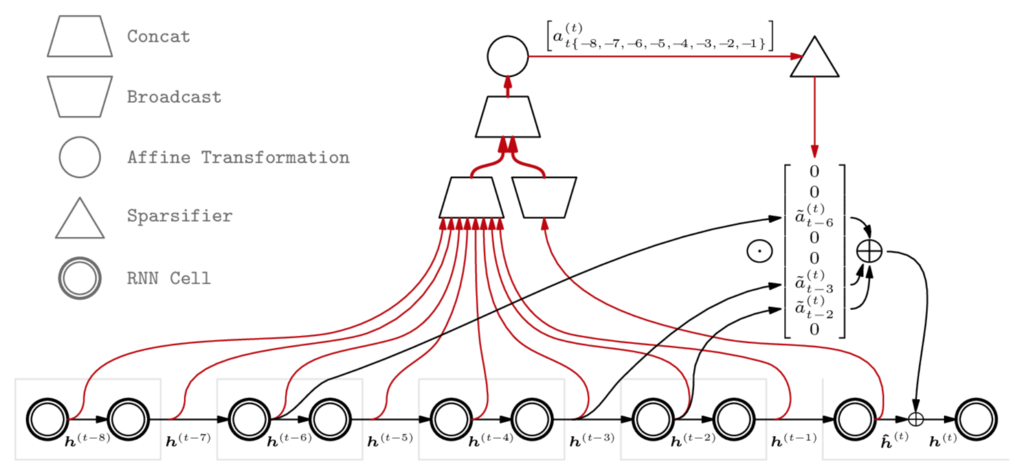
機械翻訳のエンコーダに挿入した混合エキスパート層のうち一部のエキスパートが処理した単語を周辺単語と合わせて下図に示す.

例えば第 752 番目のエキスパートは不定冠詞「a」が「重要性」や「リーダーシップ」を表す動詞句に対して直接目的語を導入するような処理に専門化している.
データ並列とモデル並列
Multi-GPU ではパラメータのロードと更新のオーバーヘッドを減らすためにバッチサイズを大きくとる必要がある.
例えば,ゲーティングネットワークが各標本につき 個中
個のエキスパートを選択し,
バッチにつき
個の標本を与えた場合,各エキスパートはおおよそ
個の標本を受け取る.これは元の
個に比べ非常に少なく,ナイーブな実装の混合エキスパートではエキスパートの数が増えるほど各エキスパートあたりのバッチサイズが小さくなり非効率である.
バッチサイズの縮小は元のバッチサイズ をできるだけ大きくとれば回避できるが,バッチサイズは順/逆伝播のネットワークを記憶するのに必要なメモリの容量によって制限されてしまう.そこで以下のような手法を提案している.
本手法ではデータ並列とモデル並列を混合して使用する.通常の層 (e.g., LSTM, ゲーティングネットワーク) では同じパラメータをコピーした各層 (各 GPU につき 1 層) にバッチを分配するデータ並列を使用し,混合エキスパート層では異なるパラメータを持った各エキスパート (各 GPU につき複数エキスパート) にバッチを分配するモデル並列を使用する.とどのつまり,各エキスパートは入力バッチから各エキスパートに関連する標本の組み合わせのみ受け取って処理する.
さっきの例で言えば,モデルを 個のデバイスに分散し,バッチサイズ
のバッチを与えた場合,各エキスパートはおおよそ
個の標本を受け取り,各エキスパートのバッチサイズは
倍の改善を達成できる.訓練クラスタの GPU 数を増やすほど比例してエキスパート数 (パラメータ数) も増大し,各エキスパート毎のバッチサイズを一定に保ちながら全体のバッチサイズも増加できる.
また言語モデルの場合,下層の LSTM が全タイムステップを終了してから 1 つの巨大なバッチを作ることで,混合エキスパートに入力するバッチサイズは LSTM のタイムステップの数だけ倍増される.
重要度損失
ゲーティングネットワークは少数の同じエキスパートに大きい重みを生成する状態に収束しやすい傾向がある.これは初期に選択されたエキスパートが急速に訓練され,ゲーティングネットワークによって更に選択されやすくなるからである.
この不均衡を回避するためにゲーティングネットワークの出力のうち閾値 を超えた成分の値を
にするハードな制約 [Eigen, 2013] や,バッチ内で活性化する各成分の分散を最大化するソフトな制約 [Bengio, 2015] が提案されている.
- Learning Factored Representations in a Deep Mixture of Experts [David Eigen, last: Ilya Sutskever, arXiv, 2013/12]
- Conditional Computation in Neural Networks for faster models [Emmanuel Bengio, arXiv, 2015/11]
本手法では重要度損失を使用したソフトな制約を使用する.
エキスパートの重要度 はゲーティングネットワークの出力をバッチ方向に総和した値によって表される.重要度に関する変動係数 (Coefficient of Variation) の 2 乗とスケーリング用ハイパパラメータ
の積を重要度損失 (Importance Loss)
と定義し,モデルの損失関数に追加する.
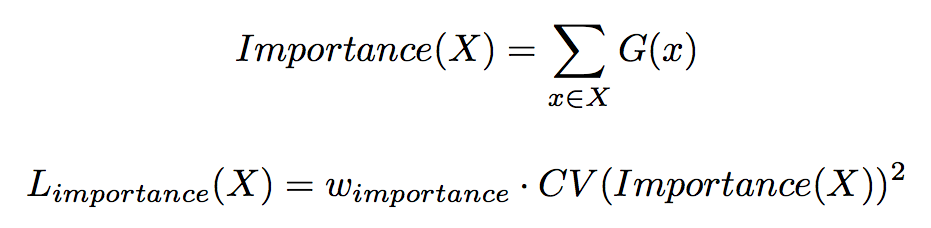
変動係数 () は「標準偏差を平均で割った値」のことで,平均が異なる 2 集団の相対的なばらつきを比較できる.今回は重要度
の各成分の値 (各エキスパートに対応) をサンプルと看做した変動係数の 2 乗を最小化するので,重要度の各成分の値のばらつきが小さくなり,全てのエキスパートが同等の重要度をもつように収束する.
負荷分散損失
重要度損失はエキスパートの重要度が等しくなることは保証するが,各エキスパートに入力される標本数が等しくなることは保証しない.例えば大きな重みで少数の標本を受け取るエキスパートと小さな重みで多数の標本を受け取るエキスパートが同等の重要度をもつ可能性がある.これは分散システムで out of memory や計算効率の悪化を引き起こす可能性がある.
残念なことに各エキスパートが受け取る標本数は離散量なので逆伝播を使用できない.代わりに「バッチ が各エキスパートに分配された標本数」の滑らかな予測器
(微分可能) を定義する.予測器を通して勾配を逆伝播することで,各エキスパートが同等の標本数を受け取るようにゲーティングネットワークのノイズ量を学習する.
まず第 成分に新しいランダムなノイズを与えたとき
が非ゼロである確率,換言すると新しいノイズ入りの第
成分が
の上位
の成分に含まれる確率
を次式のように定義する.
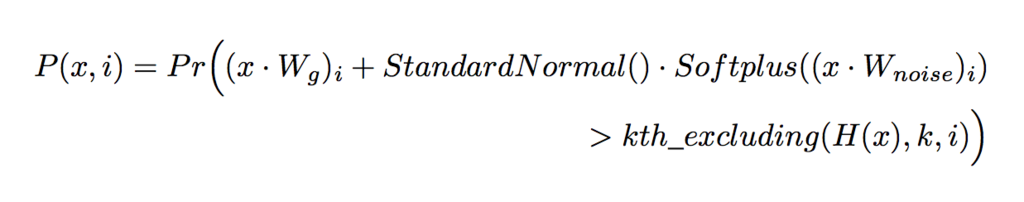
ここで は
の成分のうち成分
を除いて上位
番目の成分の値である.
これを簡略化すると次式によって表される.
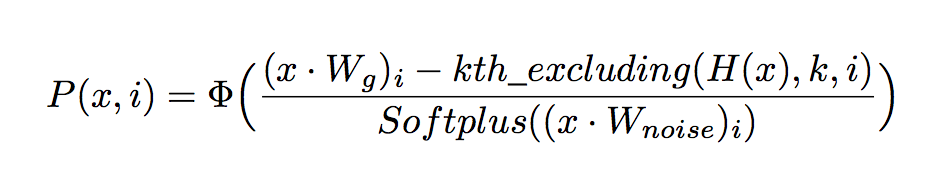
ここで は標準正規分布の累積分布関数 (Cumulative Distribution Function, CDF) であり,下図は
のプロットである.
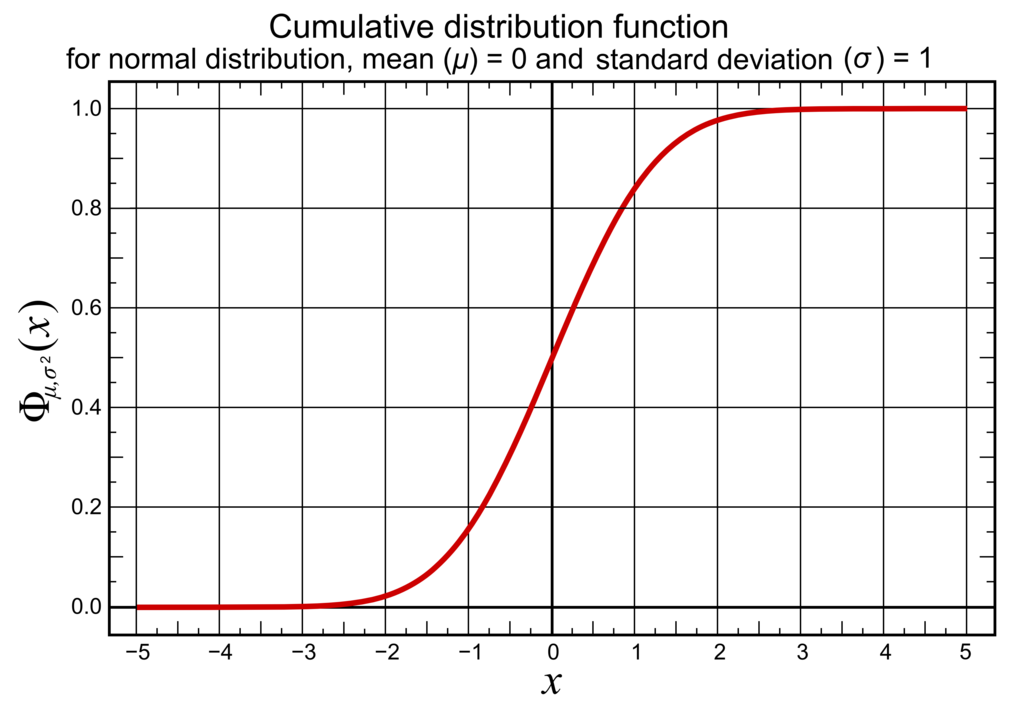
分母の Softplus (非負) が大きいほど (すなわちノイズ量が多いほど) の入力値は
に近くなるので,確率は
に近くなることが窺える.
エキスパートの負荷 は確率をバッチ方向に総和した値によって表される.
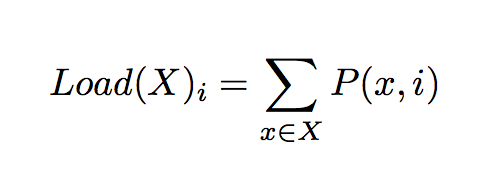
負荷に関する変動係数 (Coefficient of Variation) の 2 乗とスケーリング用ハイパパラメータ の積を負荷分散損失 (Load Balancing Loss)
と定義し,モデルの損失関数に追加する.
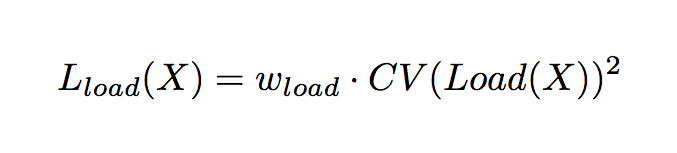
ソフトな制約は正常に動作するまでに時間がかかるので,学習初期には不均衡な負荷に起因する out of memory の恐れがある.よってエキスパートの負荷がほぼ等しい状態になるようにネットワークを初期化する必要がある.ここでは行列 と
をすべてゼロに初期化して出力を標準正規分布にのみ依存させることで分配される標本数をほぼ均等にする.
実験
ハイパパラメータ ,
の値を変えて, 256 個のエキスパートの混合エキスパート (MoE-256) を 10 エポック訓練した結果は次のとおり.それぞれテストセットのパープレキシティ,変動係数,平均負荷に対する最大負荷の割合を示している.特に最後の割合は分散システムの負荷分散のために重要である.
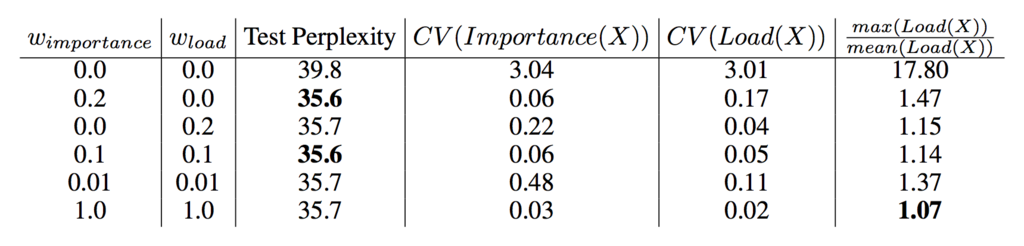
パープレキシティを比較すると重要度損失と負荷分散損失のうちどちらか一方は必須であることがわかる.
の値が高いモデルは最もエキスパートの負荷が小さくなっている.
階層的混合エキスパート
エキスパートの数が非常に多い場合,階層的混合エキスパート (Hierarchical Mixture of Experts, HMoE) を用いて分岐数を減らすことができる.第一ゲーティングネットワークでエキスパートのグループを選択し,第二ゲーティングネットワークで各グループ内のエキスパートを選択する.
- Hierarchical mixtures of experts and the EM algorithm [Michael I. Jordan, 1994]
- 階層型ネットワーク [浅川伸一, 2002]
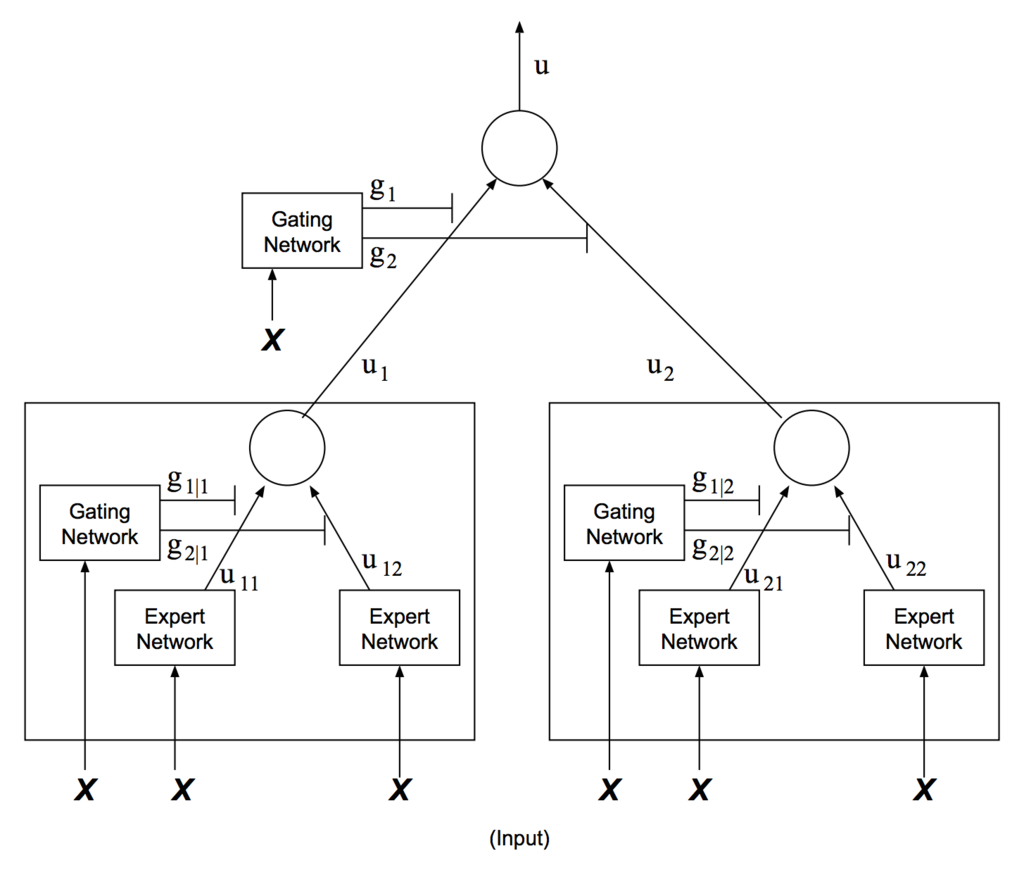
個のグループ (各グループにつき
個のエキスパート) の階層的混合エキスパートの出力は次式によって表される.
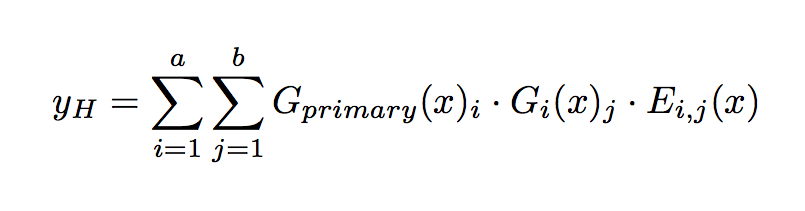
ここで は第一ゲーティングネットワーク,
は第二ゲーティングネットワーク,
はエキスパートネットワークである.
階層的混合エキスパートでは,第一ゲーティングネットワークはデータ並列,第二ゲーティングネットワークはモデル並列 ( デバイスにつき
混合エキスパート) を使用する.
言語モデルの実験結果
データセットは単語数 M,語彙数
のニュース記事 [Chelba, 2013] を使用する.
- One Billion Word Benchmark for Measuring Progress in Statistical Language Modeling [Ciprian Chelba, sec: Tomas Mikolov, arXiv, 2013/12]
モデルは 2 層の LSTM 間に MoE 層を挿入し,埋め込み層のサイズ,LSTM 層のサイズ,混合エキスパートへの入出力のサイズをすべて 512 次元に統一する.
各エキスパートは ReLU で活性化する 1024 次元の中間層と 512 次元の出力層から成る 2層の全結合ニューラルネットワークを使用する.各エキスパートのパラメータ数は100 万 () となる.
モデルサイズを増量する効果を調べるために,計算コストが等しい様々な混合エキスパートを訓練した.実験環境は 16 枚の Tesla K40 GPU で構成されたクラスタ上で TensorFlow による実装である.
それぞれ 4, 32, 256 個のエキスパートで構成される混合エキスパート (MoE-4, 32, 256),及び 256, 1024, 4096 個のエキスパートで構成される階層的混合エキスパート (MoE-256-h, 1024-h, 4096-h) を用いて 10 億単語の言語モデルを訓練した結果は次のとおり.
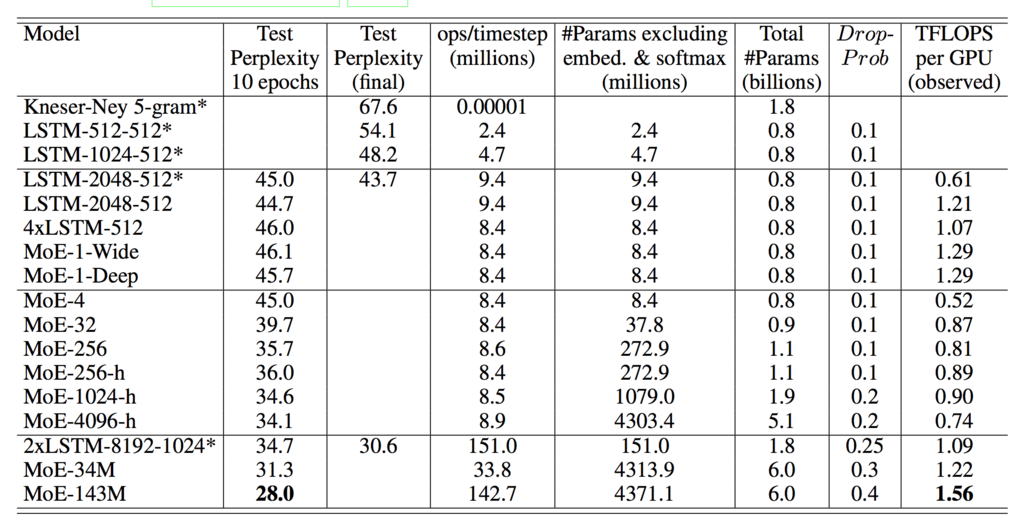
各エキスパートは約 100 万パラメータを有し,1 標本につき 4 個のエキスパートのみ活性化させた (ノイジーな上位 K ゲーティングは ,階層的混合エキスパートは第一・第二ゲーティングネットワークともに
).また,ops/timestep は 1 タイムステップの順伝播につき 1 標本に対して乗加算される操作の回数で計算効率の目安となる (1M のエキスパート 4 個 + 2M の LSTM 2 個 = 8M ops/timestep).
スパース性がない以下のベースラインはすべてパラメータ数を統一している.
- MoE-1-Wide: 4096 次元の中間層に拡大したエキスパート 1 個から成る混合エキスパート層
- MoE-1-Deep: 1024 次元の中間層を 4 層スタックしたエキスパート 1 個から成る混合エキスパート層
- 4xLSTM-512: 混合エキスパート層を 512 次元の LSTM 2 個に置き換え
- LSTM-2048-512: モデル全体を 2048 次元の LSTM 1 個 (出力を 512 次元に写像) に置き換え
4 個のエキスパートが常時活性化するモデル (MoE-4) は前述のベースラインに近い性能となった.
モデルサイズが最大のモデル (MoE-4096-h) は計算コストが等しいにも関わらずベースラインと比較して 24 %の性能向上を達成している.
巨大な混合エキスパート層の計算効率 (ops/timestep) を更に上げる効果を調べるために,2 種類のモデルを追加した (MoE-34M と MoE-143M).それぞれ埋め込み層のサイズと混合エキスパートへの入出力のサイズを 512 次元から 1024 次元に拡大し,混合エキスパート層を 40 億パラメータに増大する.
- MoE-34M: 34M ops/timestep,1024 次元の LSTM 層,2048 次元の中間層の 1024 個のエキスパートから成る階層的混合エキスパート層
- MoE-143M: 143M ops/timestep,4096 次元の LSTM 層 (出力を 1024 次元に写像),8192 次元の中間層の 256 個のエキスパートから成る階層的混合エキスパート層
それぞれテストセットのパープレキシティは 31.3 と 28.0 (登場時の SOTA) を達成し,計算効率も向上している.
機械翻訳の実験結果
Google ニューラル機械翻訳 (GNMT) を修正してモデルを構築する.
GNMT ではエンコーダとデコーダに 8 層の LSTM (エンコーダの 1 層目は双方向 LSTM) を使用した.本手法 (MoE) では計算量を減らすために 2 層の LSTM (双方向 LSTM は維持) に変更し,エンコーダとデコーダの LSTM 間にそれぞれ混合エキスパート層を挿入する.
各層の入出力はすべて 512 次元に統一し,LSTM 層と混合エキスパート層には残差接続を取り入れている.LSTM 層は 2048 次元 (出力を 512 次元に写像) を使用し,混合エキスパート層は 2048 個のエキスパートから成る 80 億パラメータの混合エキスパートを使用する.各エキスパートは ReLU で活性化する 2048 次元の中間層と 512 次元の出力層から成る 2層の全結合ニューラルネットワーク () である.ゲーティングネットワークは 1 標本につき 4 個のエキスパートのみ活性化させた (
).
希少語に対応するためにソース言語とターゲット言語で語彙を共有した 32000 ピースの wordpiece (サブワード) を使用する.
データセットは WMT'14 の英仏 (36M 対訳文) と英独 (5M 対訳文) を使用する.
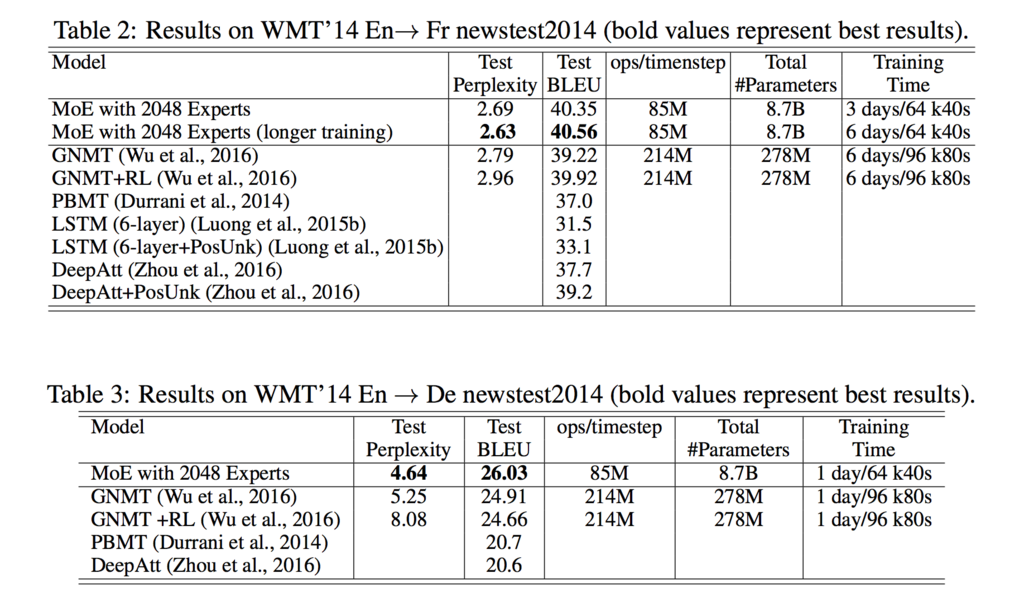
BLEU スコアは英仏: 40.56, 英独: 26.03 (登場時の SOTA) を達成した.
ゲーティングと注意の関係
ゲーティングと注意はかなり類似している.
ゲーティングと注意は と
が一対一対応する辞書オブジェクトである点で同じである.ただし注意は
と
が特徴表現であり,ゲーティングは
が特徴表現であるものの
がゲートの学習パラメータである.
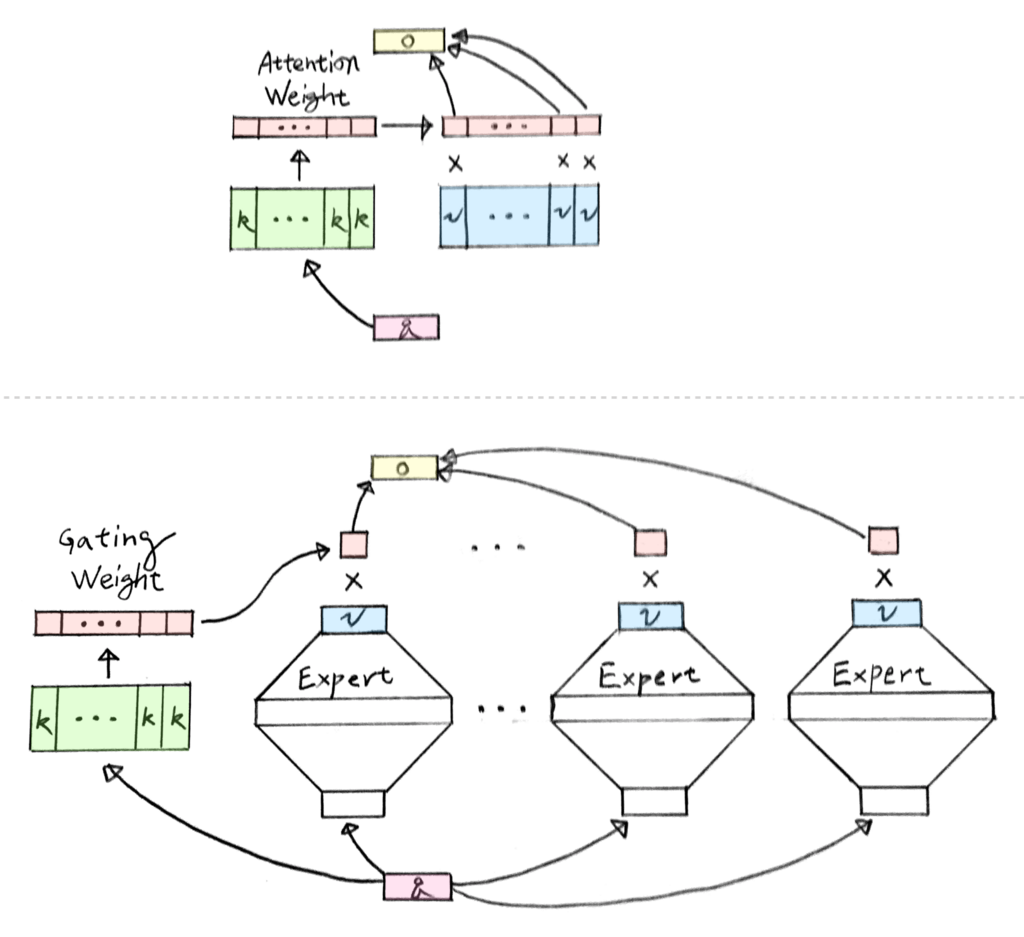
ゲーティングは「ゲーティングの重み (確率分布)」と「エキスパートの出力 (行列)」の内積を求める.一方,ソフトな注意 [Cho, 2014] は「注意の重み (確率分布)」と「メモリ (行列)」の内積を求める.
スパースゲーティングは「ゲーティングの重みから k 個をサンプリングした k-hot ベクトル」と「エキスパートの出力」の内積を求める.一方,ハードな注意 [Graves, 2014] は「注意の重みから 1 個をサンプリングした one-hot ベクトル」と「メモリ」の内積を求める.また,スパースゲーティングはサンプリングにノイズを乗せている点で Gumbel Softmax に似た効果を期待できる.
最近ではスパースゲーティング (Sparse Gating) に似たアイデアをもつスパース注意 (Sparse Attention) が提案され,今後も両者の交配が進む可能性がある.
- Sparse Attentive Backtracking: Long-Range Credit Assignment in Recurrent Networks [Nan Rosemary Ke, last: Yoshua Bengio, arXiv, 2017/11]
最後にゲーティングネットワークと LSTM, GRU, GLU 等のゲートは入力が 2 つに分岐 (コピー) するネットワーク構造という点で類似するが意外と相違点も多い.機能的には前者は「どのサブネットワークで処理するか決定するゲート」であり,後者は「どの程度情報を通すか決定するゲート (つまり感覚ゲーティング) 」である.ゲーティング自体も内積とアダマール積という点で異なる.